We've already covered the basics of tree data structure in three posts. If you haven't gone through those yet, I would strongly going through the introductory post at the very least.

Introduction

Trie is a variation of tree data structure. It's also referred to as prefix tree or a variation of search tree. Just like n-ary tree data structure, a trie can have n children stemming from single parent. Usually all the nodes in a trie would store some character. Assuming we're only dealing with English words, here's how a simple trie may look like:

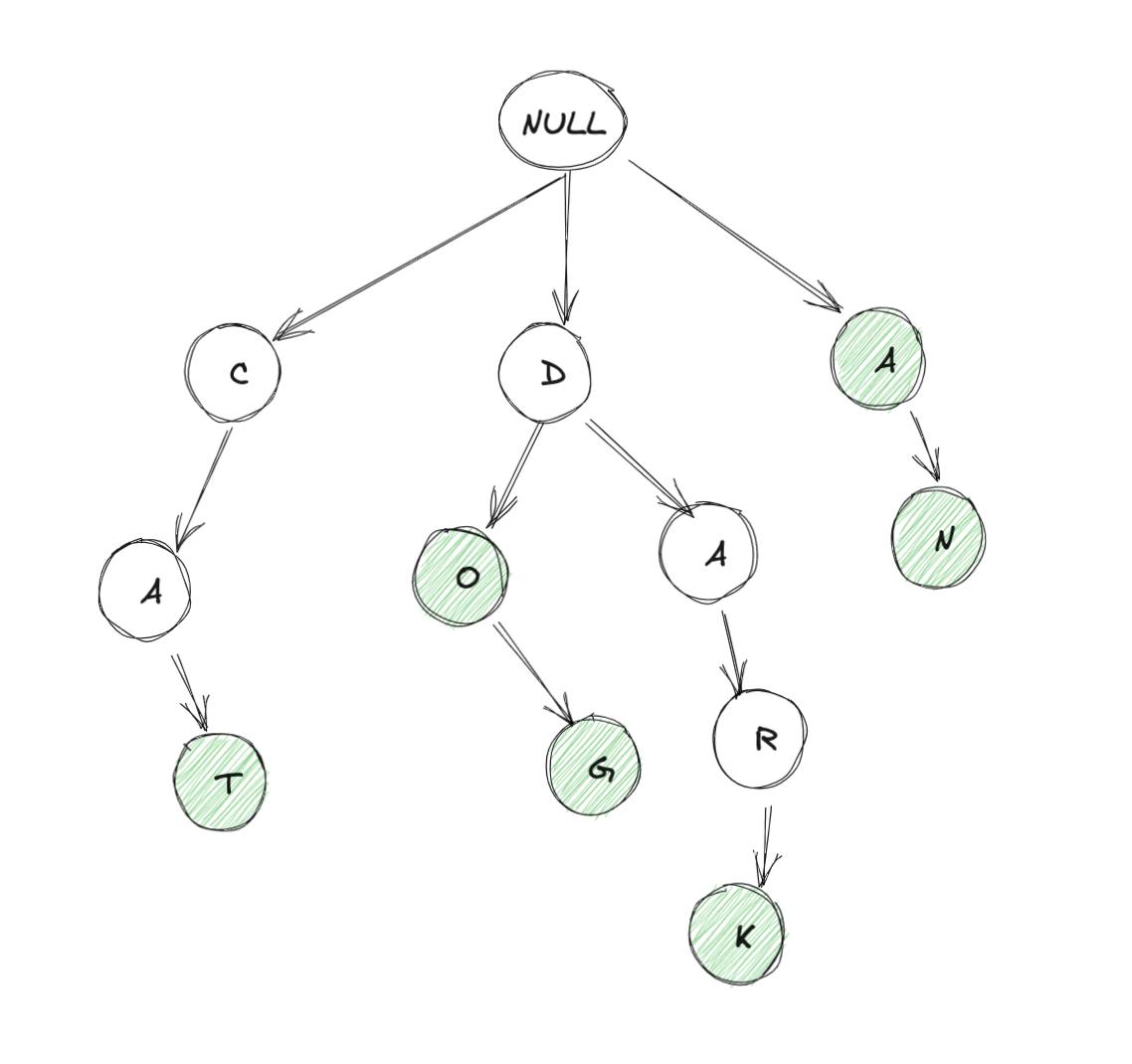
Things to note here:

1. We're trying to use a tree to represent English words here, as efficiently as possible.
2. In the diagram above, a path from root node to any of the green nodes, denotes an English word. For example:
   • NULL->C->A->T: CAT
   • NULL->D->O: DO
   • NULL->D->O->G: DOG
   • NULL->D->A->R->K: DARK
   • NULL->A: A
   • NULL->A->N: AN
3. Each node can have at most 26 children (if we're only dealing with English alphabet). We have a NULL node as root node, because a word can start with any of 26 letters hence we need a dummy node that can have any of potential first letters as a child.
4. A green node, essentially represents 'end of a word', while traversing from the root till that node.

Implement a Node

Nice! So we've got conceptual background. Now, let's try to come up with the programatic representation of the Trie node. Referring back to tree node, this is how we presented it:

function Node(value){
  this.value = value
  this.left = null
  this.right = null
}

So, we can follow a similar idea for Trie while ensuring it meets the requirements we discussed in the Introduction section. To understand requirements of a Trie node, let's zoom in on any of the nodes:

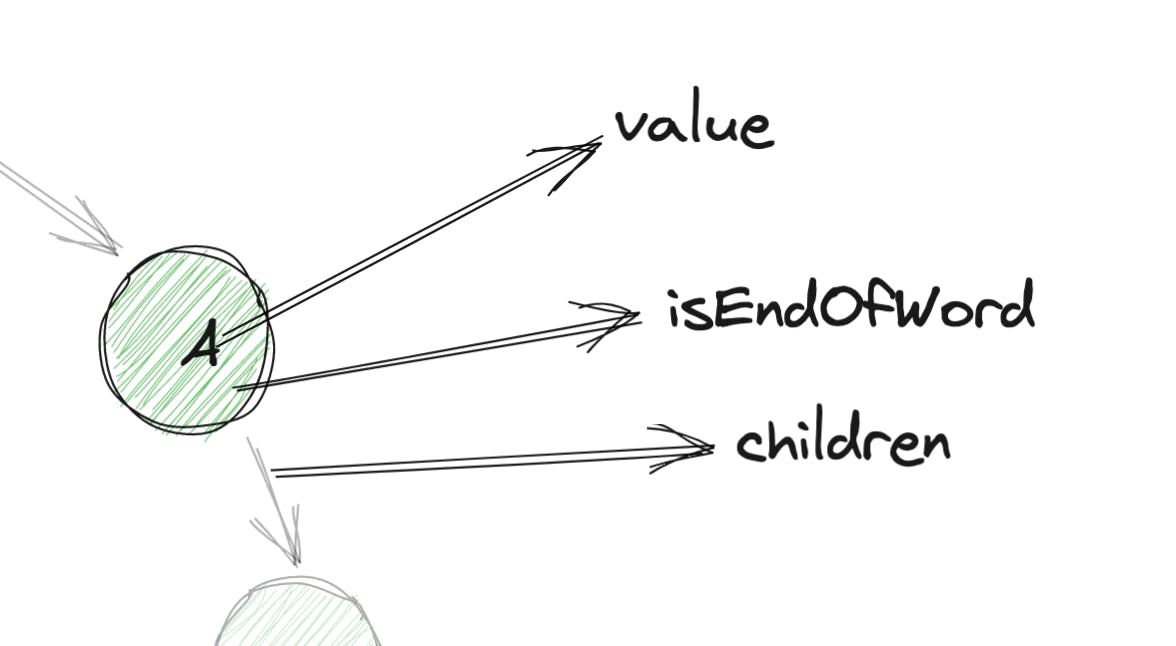
Alright, so it makes more sense now. Here's the final code:

function Node(value){
  this.value = value
  this.isEndOfWord = false // false by default, a green node means this flag is true
  this.children = {} // children are stored as Map, where key is the letter and value is a TrieNode for that letter 
}

Implementing Trie data structure

We can represent it using a simple ES6 class:

class Trie{
  constructor(){
    this.root = new Node(null)
  }

  insert(word){
   // TODO
  }

  search(word){
   // TODO
  }

}

So we've got the overall interface in place. Each trie would create it's own root node (NULL) as part of initialisation. Then we can implement the two methods as follow:

• insert(word): We can split the word into letters, and create a Node() for each of these letters. Then we can start chaining each of these Trie nodes to the root node , to insert the word. Finally we'll mark the isEndOfWord property as true for last inserted Node.

• search(word): We can split the word into letters. Then we can start looking for each of these letters one by one, starting from the root. If we're able to find all the letters sequentially, then we can return true else false.

Let's understand both the operations visually for better context:

• insert(CAR) and then insert(CAN):

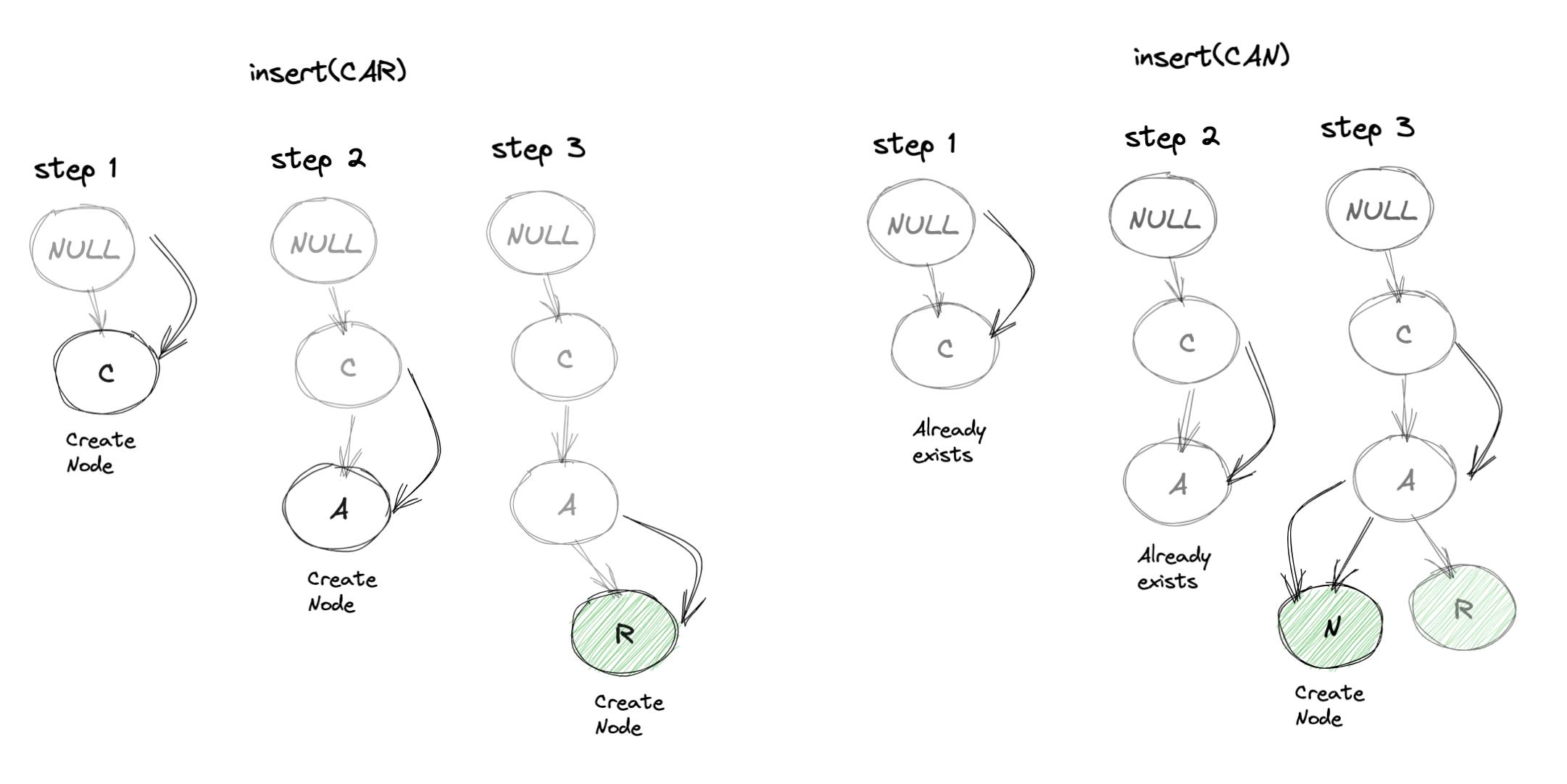
• search(CODE) and search(CAR):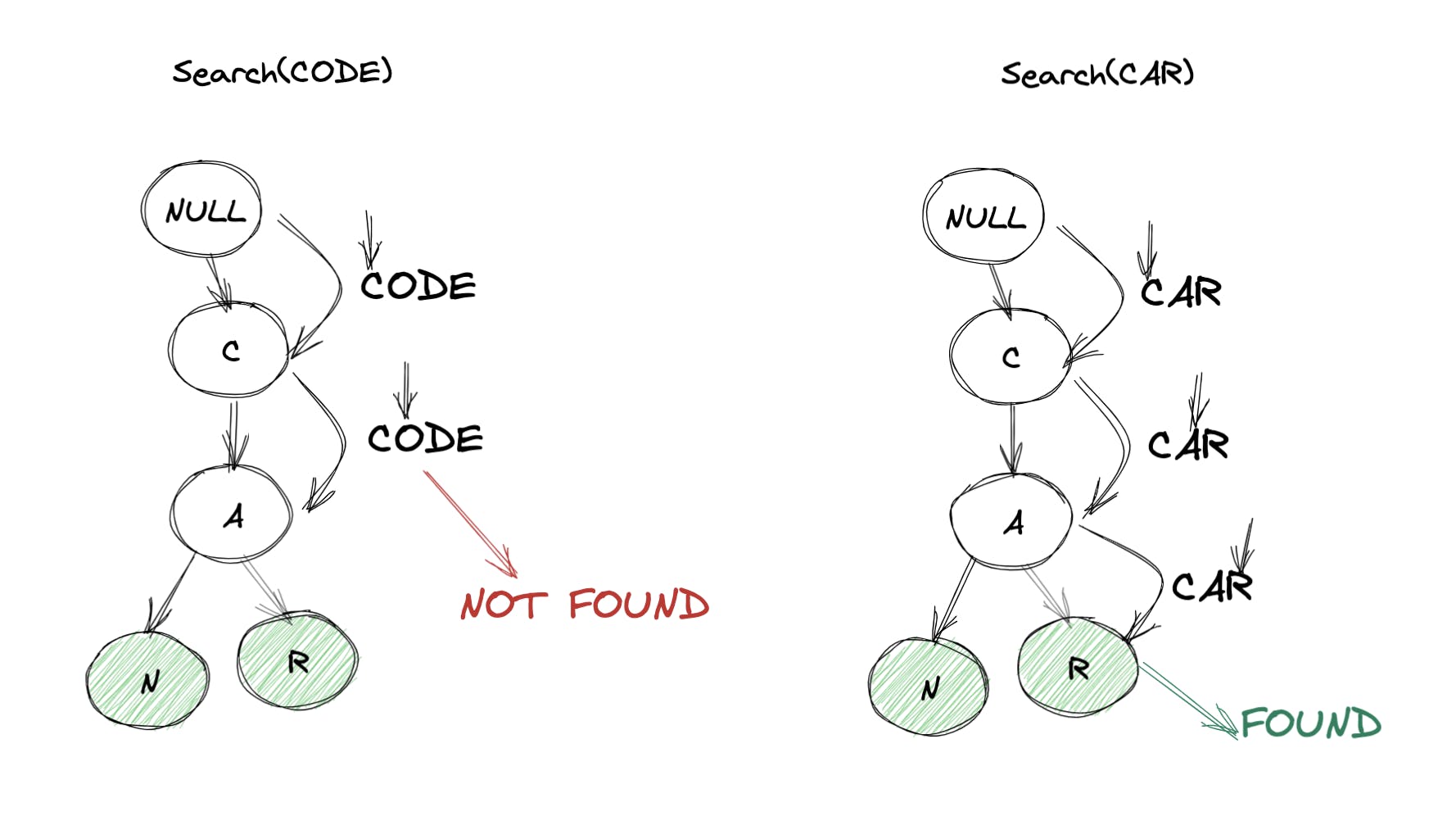

Here's how the final implementation would look like:

class Trie{
  constructor(){
    this.root = new Node(null)
  }

  insert(word){
    let current = this.root
    // iterate through all the characters of word
    for(let character of word){
         // if node doesn't have the current character as child, insert it
         if(current.children[character] === undefined){
             current.children[character] = new Node(character)
         }
        // move down, to insert next character
        current = current.children[character]  
    }
    // mark the last inserted character as end of the word
    current.isEndOfWord = true
  }

  search(word){
     let current = this.root
    // iterate through all the characters of word
    for(let character of word){
         if(current.children[character] === undefined){
             // could not find this character in sequence, return false
             return false
         }
        // move down, to match next character
        current = current.children[character]  
    }
     // found all characters, return true if last character is end of a word
    return current.isEndOfWord
  }
}

Using a Trie

Usage is straightforward. Here's a sample code showing we can use the implementation above:

const trie = new Trie();

// insert few words
trie.insert("CAT");
trie.insert("DOG");

// search something
trie.search("MAT") // false
trie.search("DOG") // true

Time and Space complexity

Space complexity:

In the worst case, each character of all inserted words can take up a single node in a Trie. So that would mean worst space complexity can be (W*n), where W is average number of characters per word and n is total number of words in the Trie.

Time complexity:

• Insert: For inserting a word having n characters, we just need to loop through n characters, so time complexity is O(n)
• Search: Similar to Insertion, we only need to loop through all the characters of the word to search it. So time complexity is O(n), where n is number of characters in the word.

Now, step back for a moment and think how else could you search for a word in a huge list of words?

• Probably using an array? Time complexity would be O(m), where where m is total number of words, which is pretty bad.
• How about using a map (or an object in JavaScript) ? Well, that would decrease time complexity to O(1), but how fast it would be to find list of words having certain prefix? It would be O(m).

Trie not only brings down the time complexity to O(n) (n = no. of characters in word), but you can also effectively search for a list of words having a prefix, which would be a much more expensive task with any of the two approaches above.

Applications

• Autocomplete and Typeahead: If you type something in a text box and you see list of potential searches with same prefix i.e. an Autocomplete widget, then that's probably being handled by a Trie behind the scenes. Similarly Typeahead can also be implemented using a Trie.

• Spell checker: We can use trie to create a spell checker i.e. given a list of words we can check if the spelling of a given word is correct or not.

• IP routing (Longest prefix matching): The Internet consists of multiple router nodes which decide the destination packet should be sent. Each router on the Internet needs to send the packet to the appropriate target node decided by the given IP destination. But how each router can decide the next destined router with the given IP address? This problem can be solved using IP routing. Here's a great article diving into this subject.