So far we've looked at implementation of tree data structure and some of it's variants such as trie. In this post, we'll dive into heaps. These are also referred to as priority queues.
Introduction
Heap is a variant of tree data structure, with two additional properties:
- It is a Complete Binary Tree: Each level of a Complete Binary Tree contains the maximum number of nodes, except possibly the last layer, which must be filled from left to right. A Complete Binary Tree is always balanced by it's definition. For reference, the diagrams below show you when a tree can be called a CBT:
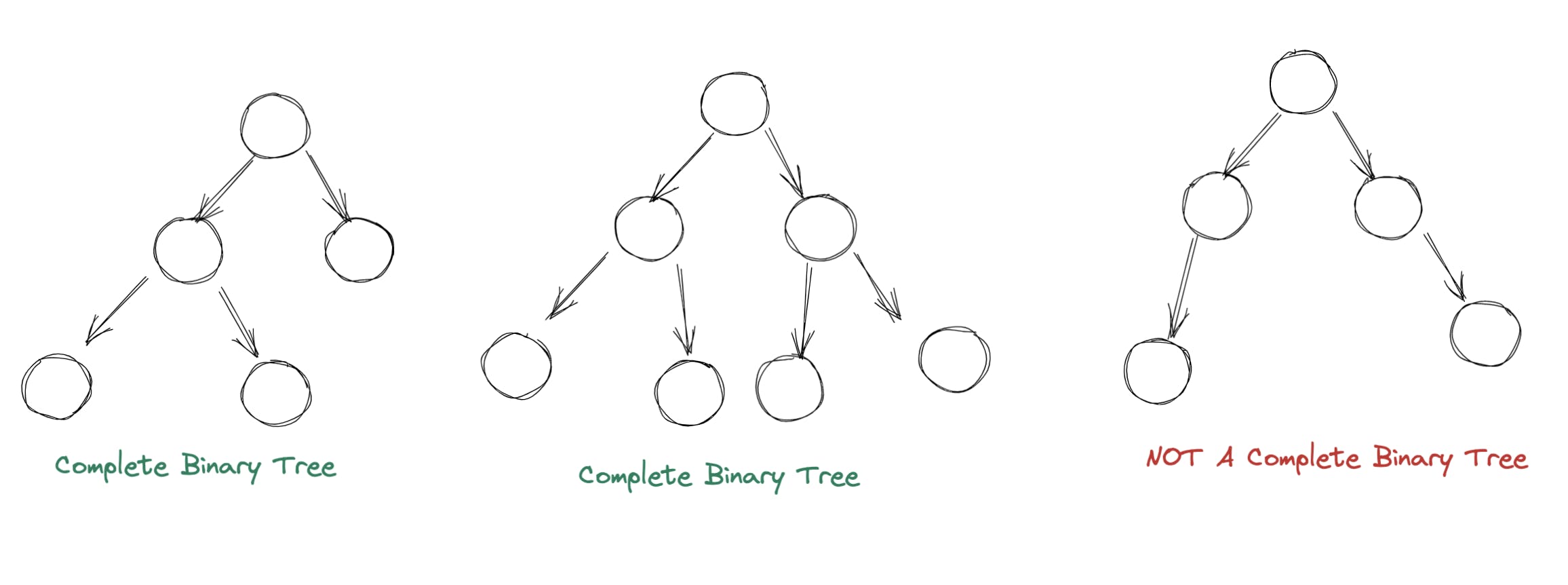
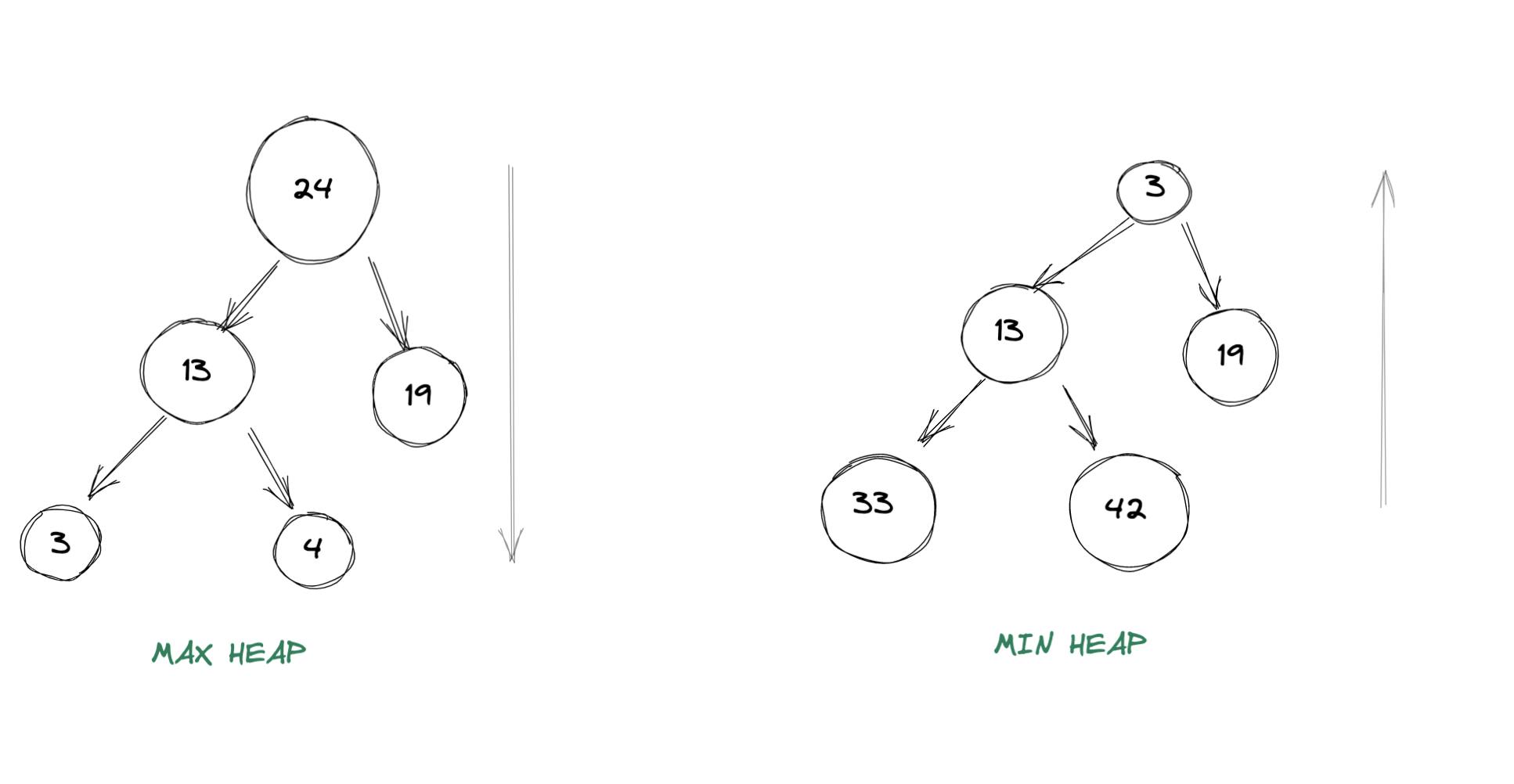
- Every node satisfies the "heap property": Heap property essentially means that for any given node C, if P is a parent node of C, then:
- For a max heap: the key of P should be greater than or equal to the key of C.
- For a min heap: the key of P should be less than or equal to the key of C.
How to represent a heap?
If you've gone through the previous posts, you'd notice we usually start implementation with class representation of a node and then tie it up with class representation of the actual data structure itself. We can do the same for heaps as well. However, there's a simpler way of solving this problem, which is because of the one of the two properties that all heaps must abide by:
All heaps must be Complete Binary Trees
Since all heaps must be Complete Binary Trees and we know that all levels, excepts last one, in Complete Binary Tree must be completely filled. Also, for the last level, all children must be filled from left to right direction, without any gaps. This definition ensures that a Complete Binary Tree of n nodes can only have 1 possible shape. It, in turn, would allow us to represent the Complete Binary tree using an array. Which means, heaps can be represented using arrays too. For example, we can represent a simple heap as an array, as illustrated below:
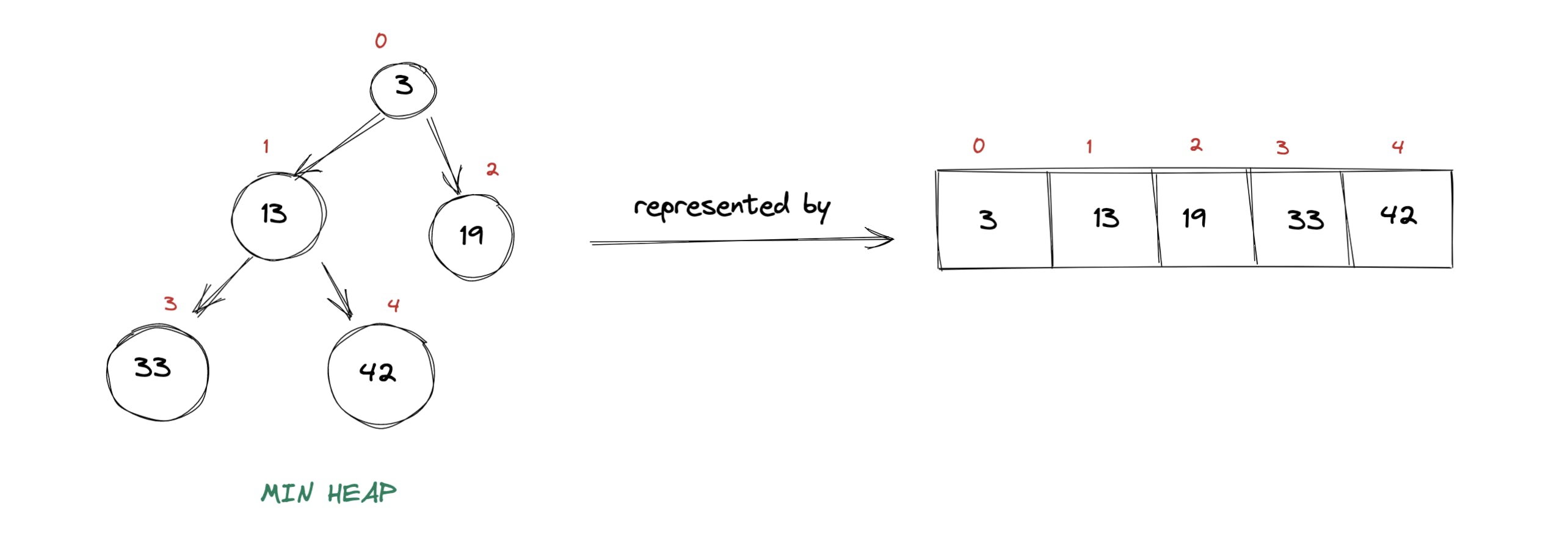
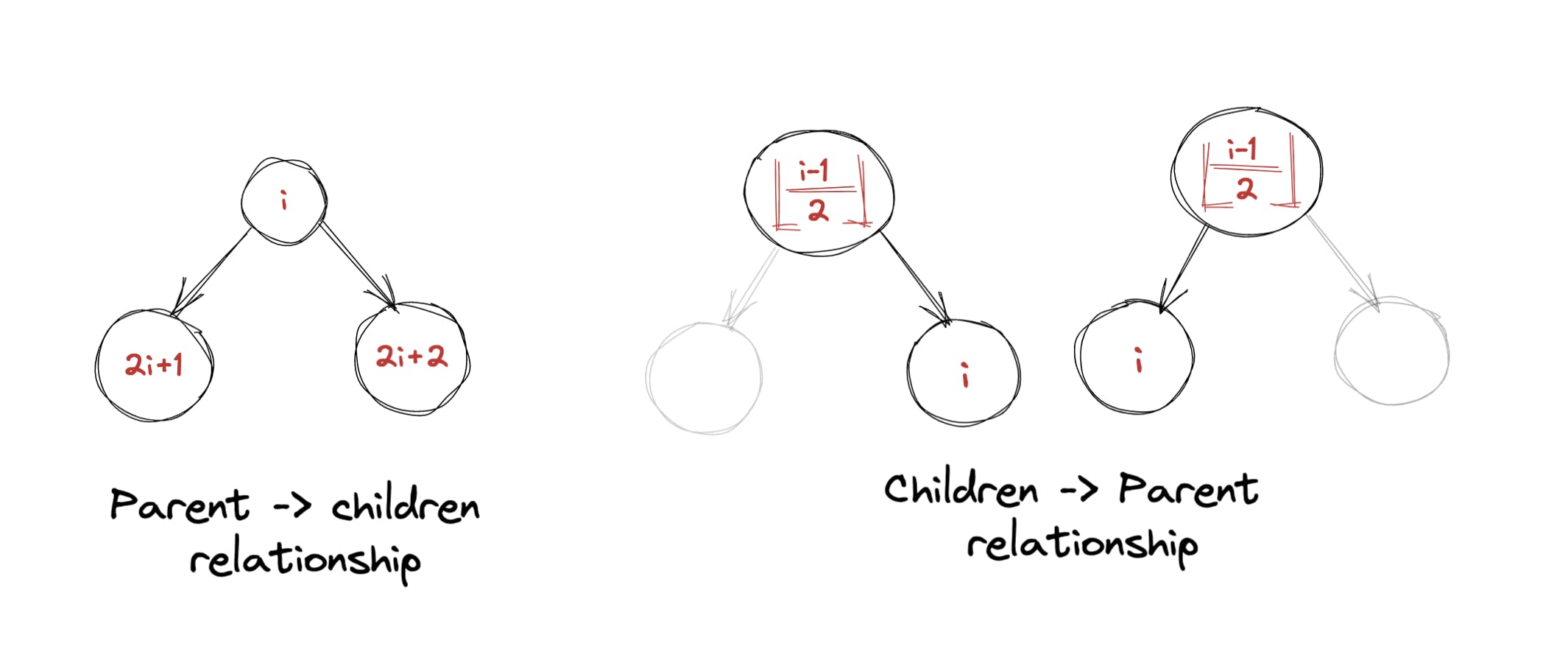
Key thing to note here is the relationship between parent and children nodes. If you look closely at the diagram above, we can deduce following:
- If a node is placed at index i in array, then given that the resultant index lies within length of the array:
- It's left child would be at (2i+1)th position
- Right one would be at (2i+2)the position
- If a node is placed at index i in array, it's parent node would be located at
floor((i-1)/2)th index.
Diagram below makes it easier to consume the info above:
Preparing the interface
Note: throughout the implementation we'll only be talking about min-heap. We'll later see that how the same idea can be easily extended to max-heap as well.
Now that we've covered the representation details, let's come up with an interface for using the data structure. There are three key things we want to be able to achieve with the help of our heap data structure:
- Add a new key into the heap
- Remove the max or min key from the heap (depending on whether it's min heap or max heap)
- Get the max of min key from the heap (depending on whether it's min or max heap)
Third operation is quite trivial. We know for the min heap, first item in the array would be the min key and similarly for max heap, first item in the array would max key. So we're left with implementation of two operations:
// adds the provided newKey into the min-heap named "heap"
function heappush(heap, newKey){}
// removes the smallest key from the min-heap named "heap"
function heappop(heap){}
Implementing heappush()
How can we add a new key into the heap? Let's say we start by pushing the new key into the array. Pushing the new key still let's us abide by the first requirement of the heap i.e it must be a Complete Binary Tree. However, we need to ensure that it abides by the "heap property" as well.
We can do so by comparing the pushed item with it's parent. If parent is larger than the pushed item then we know heap property is being violated, hence we can swap. We can continue doing this swapping until a legal parent is found or we've reached top of the heap. Here's a visual guide for better reference:
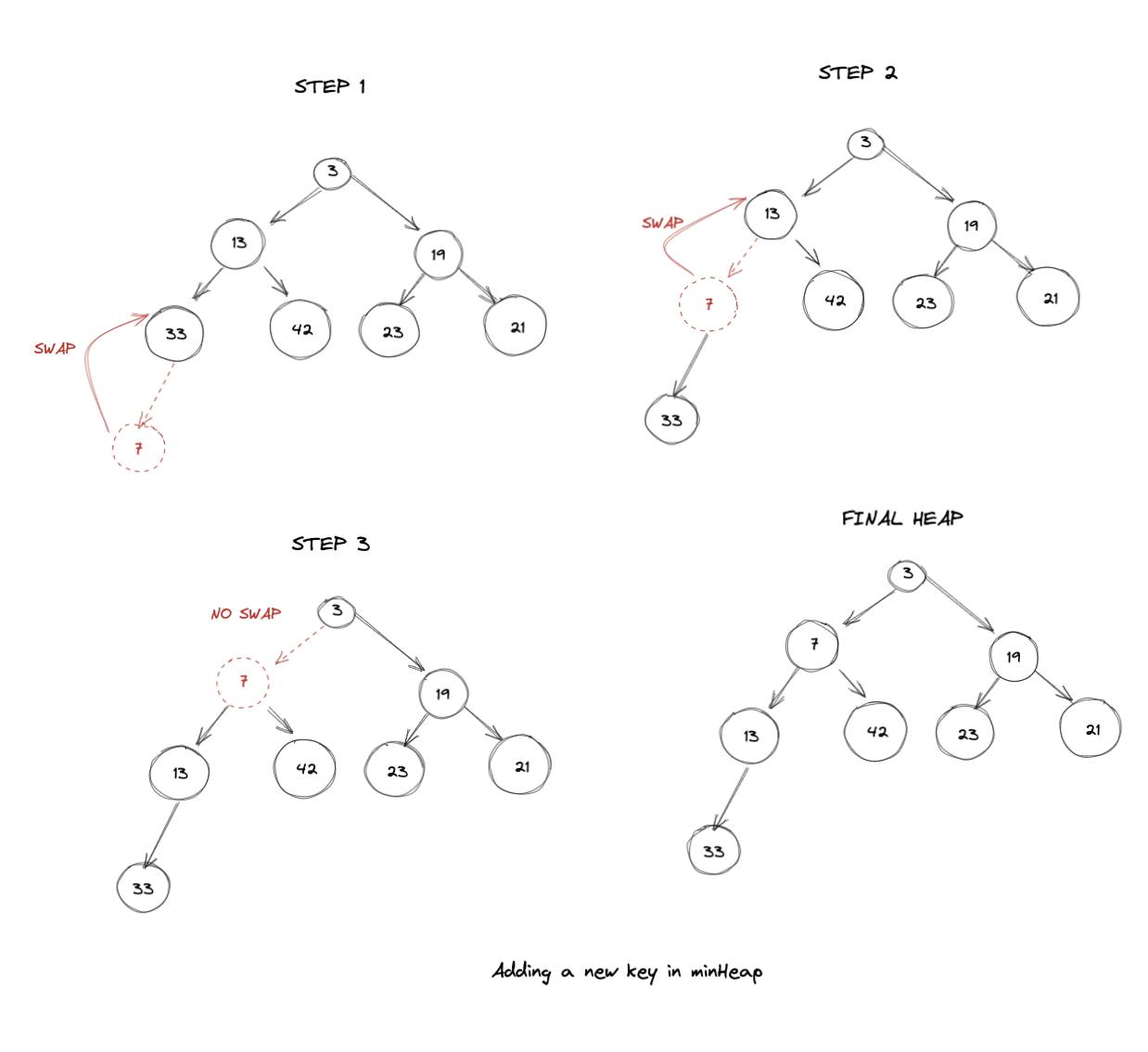
Here's the final implementation:
function heappush(heap, newKey){
// push the new key
heap.push(newKey);
// get the current index of pushed key
let curr = heap.length-1;
// keep comparing till root is reached or we terminate in middle
while(curr > 0){
let parent = Math.floor((curr-1)/2)
if( heap[curr] < heap[parent] ){
// quick swap
[ heap[curr], heap[parent] ] = [ heap[parent], heap[curr] ]
// update the index of newKey
curr = parent
} else{
// if no swap, break, since we heap is stable now
break
}
}
}
Implementing heappop()
Using heappop() we need to remove the topmost item of the heap. Meaning, for a min-heap the minimum key would be removed and for a max-heap maximum key would be removed. From the perspective of array, it simply means we should remove the first item of the array. But then which node should become the root ? If we randomly choose either of left or right children of the removed node, as new root node, that wouldn't guarantee following the heap property.
We can follow these steps instead (for a min-heap):
- Swap the root node with last node (first item with last item in the array)
- Remove the root node by popping the last item out of the array
- Compare the new root node's key with it's children:
- If key is less than both of it's children keys then heap is stable
- Else, swap the key with the smaller child key
- Repeat step 3 until last child is reached or the heap property is established.
Essentially we're following a similar process as heappush(), except we're trying to establish the heap-property in top to bottom fashion i.e. start with the root and keep going till last child. In heappush() we followed opposite order i.e. start from the last child and keep going till the root.
Here's how the actual implementation looks like:
function heappop(heap){
// swap root with last node
const n = heap.length;
[heap[0], heap[n-1]] = [ heap[n-1], heap[0]]
// remove the root i.e. the last item (because of swap)
const removedKey = heap.pop();
let curr = 0;
// keep going till atleast left child is possible for current node
while(2*curr + 1 < heap.length){
const leftIndex = 2*curr+1;
const rightIndex = 2*curr+2;
const minChildIndex = (rightIndex < heap.length && heap[rightIndex] < heap[leftIndex] ) ? rightIndex :leftIndex;
if(heap[minChildIndex] < heap[curr]){
// quick swap, if smaller of two children is smaller than the parent (min-heap)
[heap[minChildIndex], heap[curr]] = [heap[curr], heap[minChildIndex]]
curr = minChildIndex
} else {
break
}
}
// finally return the removed key
return removedKey;
}
Creating a heap using an exisiting array
Creating a heap from a pre-existing array looks pretty simple. Just create an empty heap and then iterate through all items of the array and perform heappush():
function heapify(arr){
const heap = []
for(let item of arr){
heappush(heap, item)
}
return heap;
}
But can we do slightly better here? Yes. First off, we can avoid using extra space for the new heap altogether. Why not just re-arrange the items of the array itself so that it satisfies the heap property? To do this we can follow a similar logic as we did for heap pop. We can look at the first node and compare to it's children to see if it's the smallest one, if not swap it with the smaller child. In fact let's create a function for that called percolateDown(), since we're moving downwards:
// follows pretty much the same logic as heappush, except minor modifications
function percolateDown(heap, index){
let curr = index;
// keep going down till heap property is established
while(2*curr + 1 < heap.length){
const leftIndex = 2*curr+1;
const rightIndex = 2*curr+2;
const minChildIndex = (rightIndex < heap.length && heap[rightIndex] < heap[leftIndex] ) ? rightIndex :leftIndex;
if(heap[minChildIndex] < heap[curr]){
// quick swap, if smaller of two children is smaller than the parent (min-heap)
[heap[minChildIndex], heap[curr]] = [heap[curr], heap[minChildIndex]]
curr = minChildIndex
} else {
break
}
}
Alright. So now, we can use the percolateDown() function for all items of the array one by one to put everything in correct order as per heap-property:
function heapify(heap){
for(let i in heap){
percolateDown(heap, i)
}
return heap
}
So that saves us an extra array. But can we do anything to improve time taken? Yes. If you look closely we're actually doing some repetitive work here. Say there are n nodes in heap, out of which x are leaf nodes then that means we only need to perform percolateDown() for n-x nodes, since last x nodes would be in correct place by then.
Great! So in the array representation of heap, till which index we should perform the percolateDown() operation? Well, till the index where parent of the last node lies. Because as soon as parent of last node is percolated down it'll take care of the last node too. So:
- If array length is
n - Last node's index would be:
n-1 - It's parent node's index would be:
Math.floor((n-1) - 1 / 2) = Math.floor(n/2 - 1)
Hence our final heapify function would be:
function heapify(heap){
const last = Math.floor(heap.length/2 - 1);
for(let i = 0; i <= last; i++){
percolateDown(heap, i)
}
return heap
}
Time and space complexity
Looking at the heappush() and heapop() operation, it's apparent that we're running through the height of the tree while trying to add or remove a key. Since heap is a balanced tree, height is log(n) where n is total number of nodes. Hence for push and pop operations of heap the time complexity would be O(log(n)). The time complexity for heapify() operation may seem like Onlog(n), since each call takes O(log(n)). This observation is correct for deriving the upper bound of the time complexity for heapify(), however, the asymptotic (averaged) time complexity comes out to be O(n). More details on this here. In terms of space complexity, it's constant, since extra space is only being taken up by the constant-sized variables like curr, leftIndex etc.
What about max-heap?
If we've an implementation of minHeap we can easily use it as a max heap as well. We just need to ensure that while adding values to the heap we insert negative of the key. It would ensure that heap acts as min-heap for negative of all the keys which is equivalent to maxHeap for all the actual keys. Example:
- Say we have an array
const x = [23, 454, 54, 29]; - Min-heap can be created using:
const heap = [];
for(let el of x) heappush(heap, el);
// min value
const min = heappop(heap)
- Max-heap can be created using:
const heap = [];
for(let el of x) heappush(heap, -el);
// max value
const max = -heappop(heap)

