In the first part of this series we looked at recursive and iterative approaches for traversing through a binary tree. If you haven't looked through it yet, I highly recommend you to check it out first. I'll wait here, I promise ;)

In real life applications, it's quite common for tree nodes to have a parent field: a field which points to the parent node, hence also called as the parent pointer. Let's take the example of DOM in browser. Say we select any node using the following:

const element = document.querySelector("#id")

Now, we would find element.parentNode to be pointing to the element's parent.

In this article, we'll look at how we can use these parent pointers to make the traversal more efficient. I'll explain what do I mean by 'more efficient' in a bit. In the next article, we'll also see how we can use the lessons learnt here to create myQuery library (a lightweight jQuery clone) from scratch.

Updating our Node definition:

First off, we need to update our Node function (side-note: in OOPs world you may call this a class instead, because this function is always to be invoked with the new operator):

function Node(value){
  this.value = value
  this.left = null
  this.right = null
  this.parent = null // added parent field
}

Nothing fancy here! Now let's see how we can use this new Node definition to create a similar tree, as we did in last article.

const root = new Node(2)

const left = new Node(1)
root.left = left
left.parent = root

const right = new Node(3)
root.right = right
right.parent = root

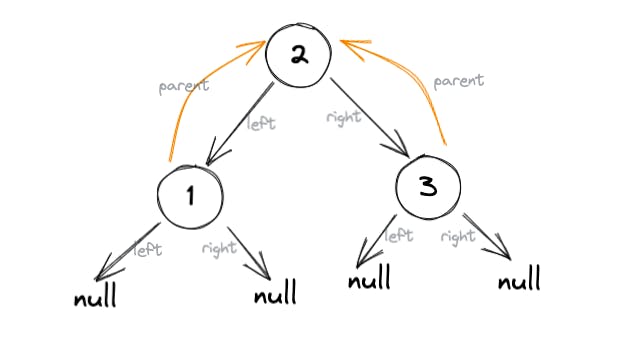
Alright so that was simple too. We simply needed to ensure parent fields point to the parent node. Here's a visual reference for the final tree we get using the code above:

Finding the successor

PreOrder successor

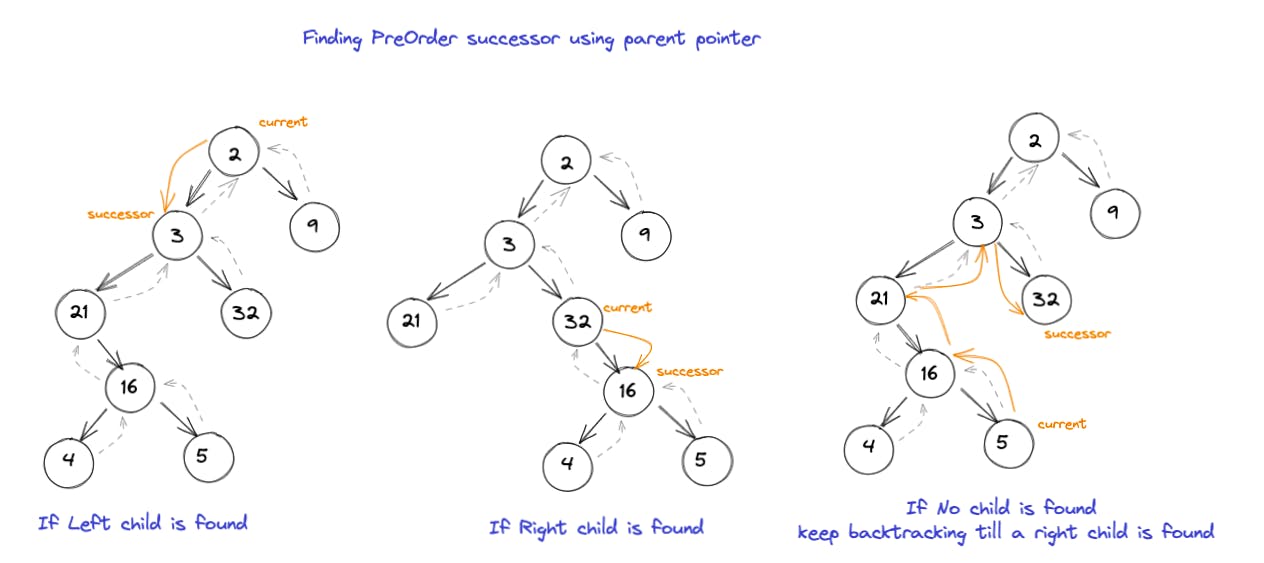
Let's do something more fun. How about finding the next node in preOrder traversal of tree given the current node and the fact that each node has a parent pointer. Let me rephrase this question for clarity:

How can be find out the preOrder successor of any node in a binary tree? Assume that each node has a parent pointer.

Let's try to dissect this problem.

1. First off, we're dealing with preOrder here, that means we're looking for following order:

   root -> left -> right
   

2. That means if we're already at current node, we want to look for the left child node as successor.
3. What if there's no left child at all ? Well in that case, we look for the right child and if it's there, that's the successor.
4. If there's no left or right child, then we need to backtrack (keep going upwards towards the parent). We keep backtracking till parent is being reached via it's right child (because that means preOrder is complete for whole subtree under the parent, by definition on #1).

So here's what the final algorithm would look like:

function preOrderSuccessor(node){
   if(!node) return

   if(node.left) return node.left
   if(node.right) return node.right

   let parent = node.parent

   while(parent && parent.right === node) {
     node = node.parent
     parent = parent.parent
   }

   if(!parent) return null // we backtracked till root, so no successor

   return parent.right
}

Here's the visual cue for better understanding.

Here's a link to a gist on this idea, in case you want to explore it for yourself.

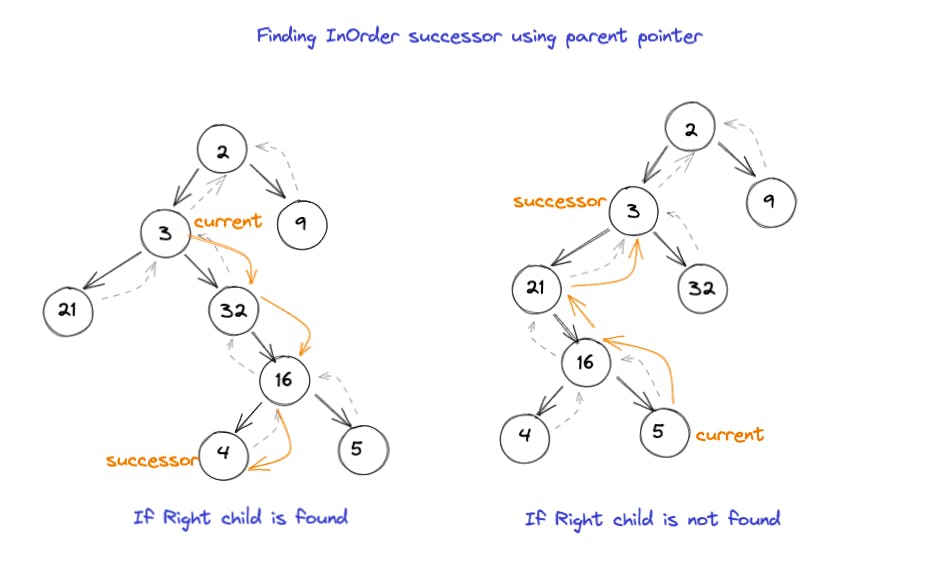
InOrder successor

Finding InOrder successor is pretty similar. Let's go step by step:

1. For InOrder successor we are looking to traverse in following way:

   left -> root -> right
   

2. If we're at current node, and there's anything on it's right then we can get the successor by finding the leftmost node on the right subtree.

3. If there's no right child, then we need to backtrack (move upwards). We keep moving upwards till parent is reached via it's right child, because that means whole subtree has been traversed already (by definition in #1).

4. Once we find the nearest parent, which has been found via it's left child, this it is returned as the successor. Why? Because it means it's a node whose left tree has been explored, so by definition in #1, the node itself is now the successor.

Here's the final algorithm:

function inOrderSuccessor(node){
   if(!node) return

   if(node.right){
     let current = node.right
     while(current && current.left) current = current.left
     return current
   }

   let parent = node.parent

   while(parent && parent.right === node) {
     root = node.parent
     parent = parent.parent
   }

   if(!parent) return null

   return parent
}

Visual cue:

Link to gist on this idea.

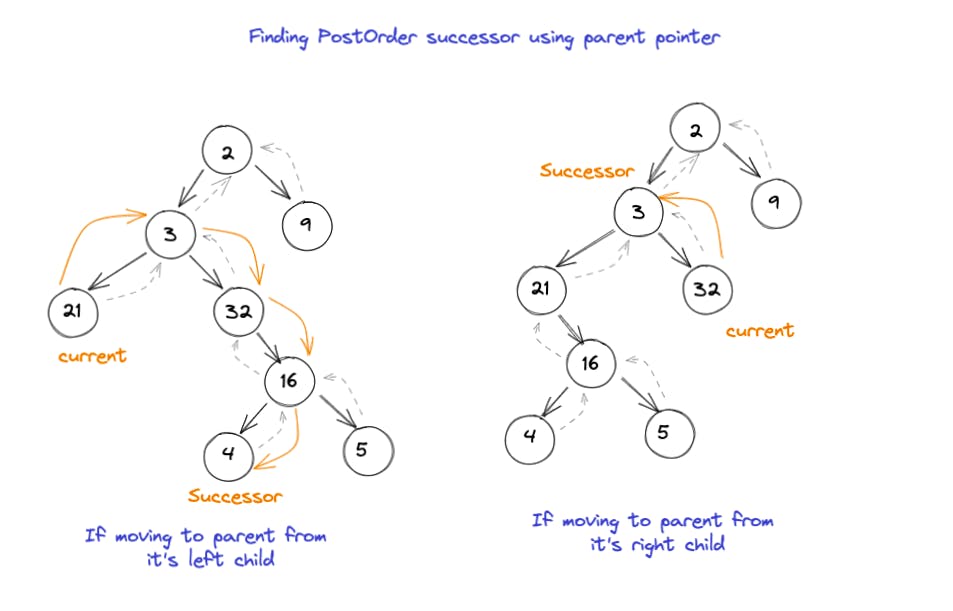
PostOrder successor

Let's follow similar thought process for finding the postOrder successor:

1. For postOrder, we are looking to traverse in following way:

   left -> right -> root
   

2. So, if we're at any node it means it's left and right subtree has already been explored. That means we need to look at the parent for successor.

3. If we're reaching the parent from it's right child, that means parent itself is successor, by the definition in #1

4. If we're reaching the parent from it's left child, that means parent's right child is to be explored next (as per definition in #1). So now we need to simply return the leftmost node in parent's right child as successor.

Here's the final algorithm:

function postOrderSuccessor(node){
   if(!node) return

   let parent = node.parent
   if(!parent) return null

   if(parent.right === node). return parent

   let current = parent.right
   while(current && (current.left || current.right)){
     current = (current.left || current.right)
   }

   return current
}

Link to gist to play around with this idea.

Using successor algorithms for better traversal

Why ?

Why do we need to use parent field to come up with a traversal algorithm at all? It's a valid question, since we've already come up with recursive and iterative approaches to traverse the tree, that too without the need for parent field.

The reason why we're doing this is because of added space complexity in our previous approaches. If you remember we needed to use one or two stacks (depending on traversal method) in the previous article, to get any of the traversal algorithms working. Even in recursive approach, though we're not directly using a stack but recursion itself is based on call-stacks, so there's hidden in-memory stack being used there as well. The problem is that size of this stack is going to increase with depth of our tree, hence it's not the best solution since we've a way to do the same task while spending lesser space . By using the parent pointer we can get rid of those stacks completely, saving us significant space i.e. going from space complexity of O(logN) where N denotes size of a balanced tree to O(1). Let's see how.

PreOrder traversal

For preOrder traversal, we start at the root of the tree. Afterwards, we can keep fetching the preOrder successor using the algorithm above to traverse the whole tree:

function preOrder(root){
  // first node
  console.log(root.value);

  let current = root
  while(true){
    const next = preOrderSuccessor(current)
    if(!next) break

    // do something
    console.log(next.value)

    current = next
  }
}

InOrder traversal

For InOrder traversal, starting node would be the left-most node of the tree. Thereafter we can keep fetching the successor using the algorithm above to traverse the whole tree:

function inOrder(root){
  // start at the left most node
  while(root && root.left){
    root = root.left
  }

  // first node
  console.log(root.value);

  let current = node
  while(true){
    const next = inOrderSuccessor(current)
    if(!next) break

    // do something
    console.log(current.value)

    current = next
  }
}

PostOrder traversal

Very similar to InOrder approach above:

function postOrder(root){
  // start at the left most node
  while(root && root.left){
    root = root.left
  }

  // first node
  console.log(root.value);

  let current = node
  while(true){
    const next = postOrderSuccessor(current)
    if(!next) break

    // do something
    console.log(current.value)

    current = next
  }
}

Quick exercise

Can you come up with algorithms for finding predecessor (inOrder, preOrder and postOrder) if each node has a parent pointer ? It would be a fun exercise. Try it out and let me know in the comments.